Soft Body Engine

A work in progress interactive Physics Engine, using Macroquad to handle the graphics and egui for the UI. Especially focused on basics of soft-body mechanics.

Interaction

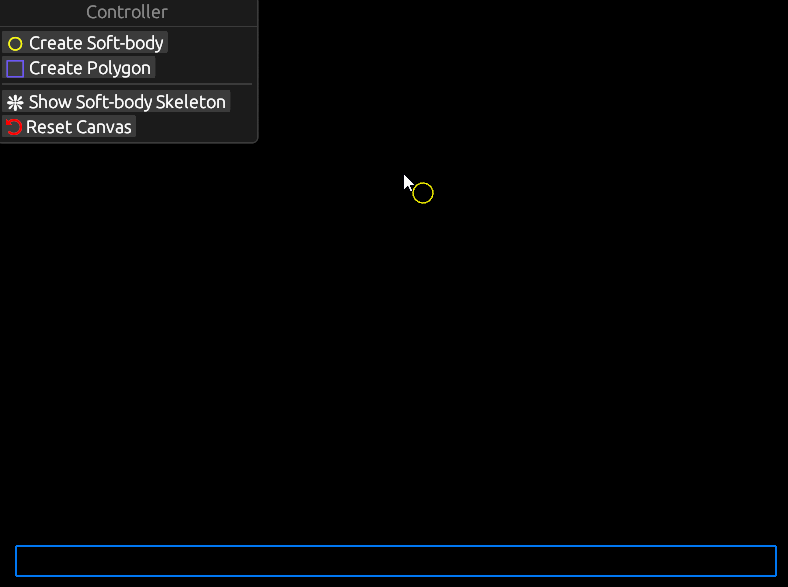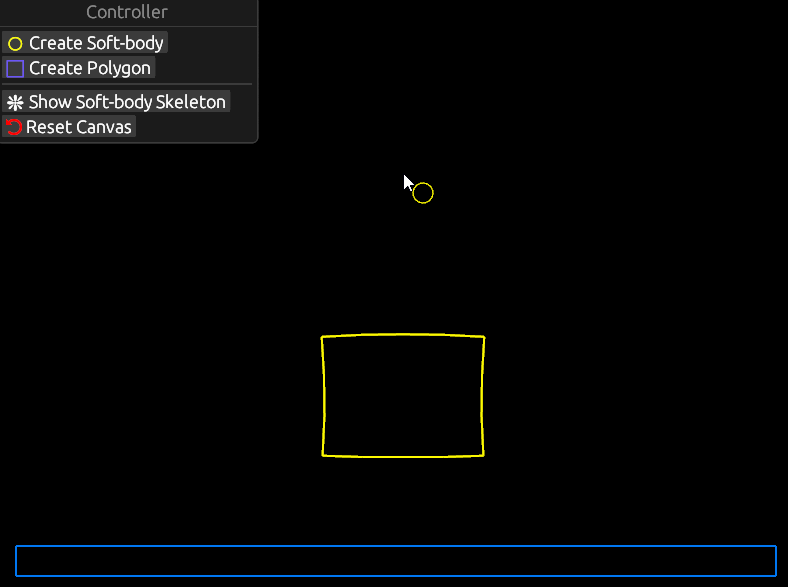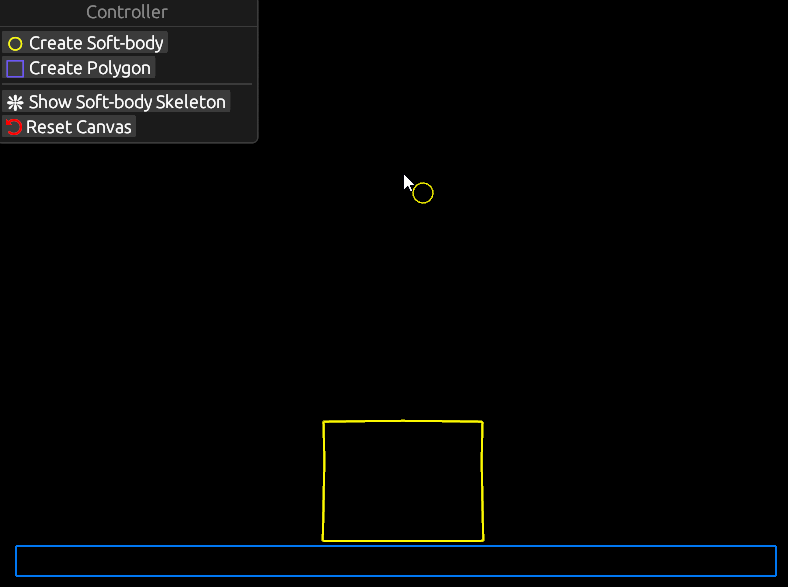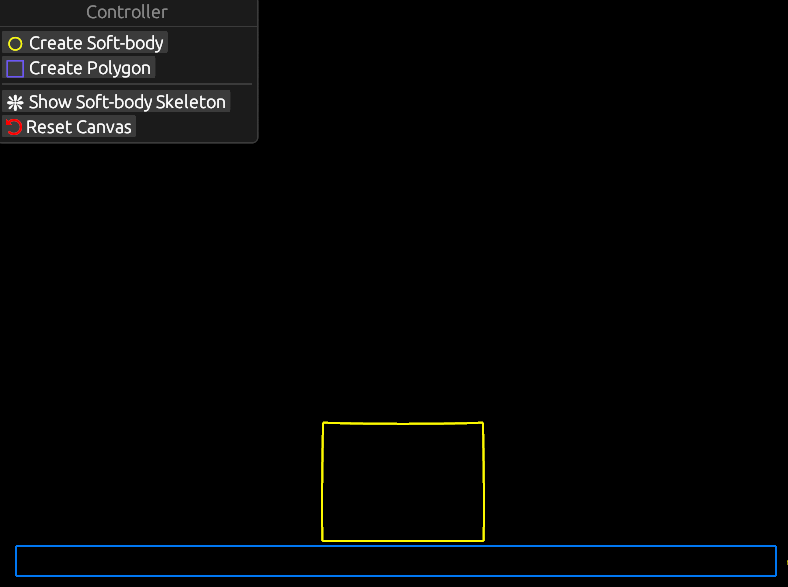
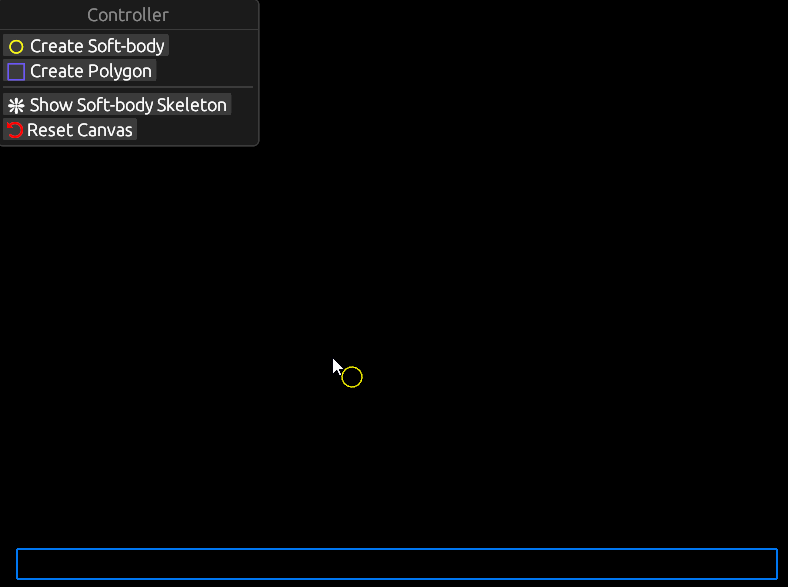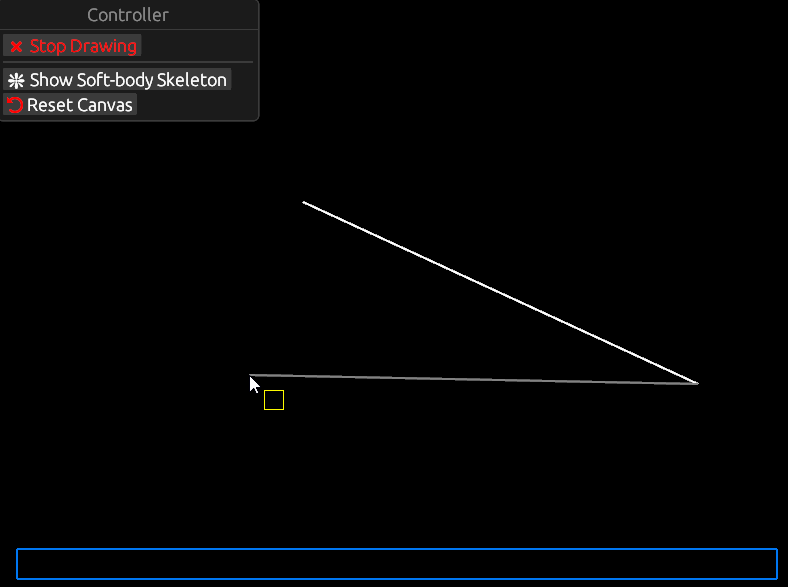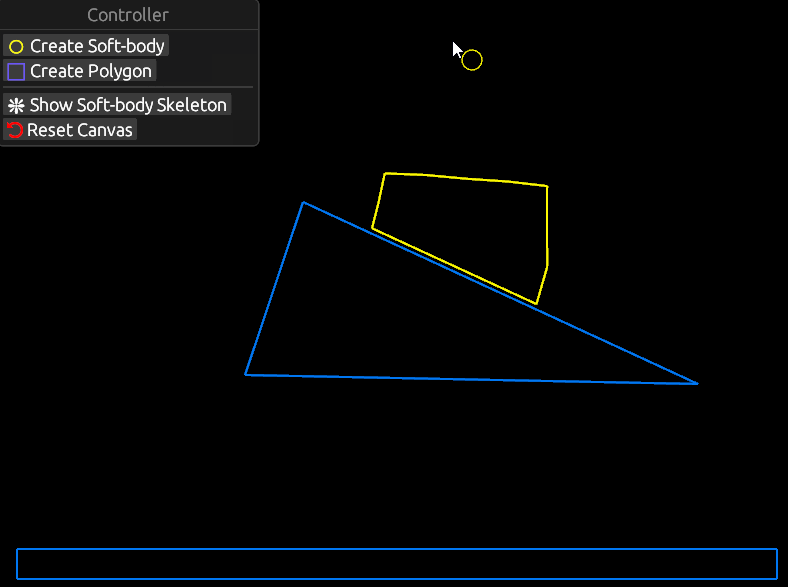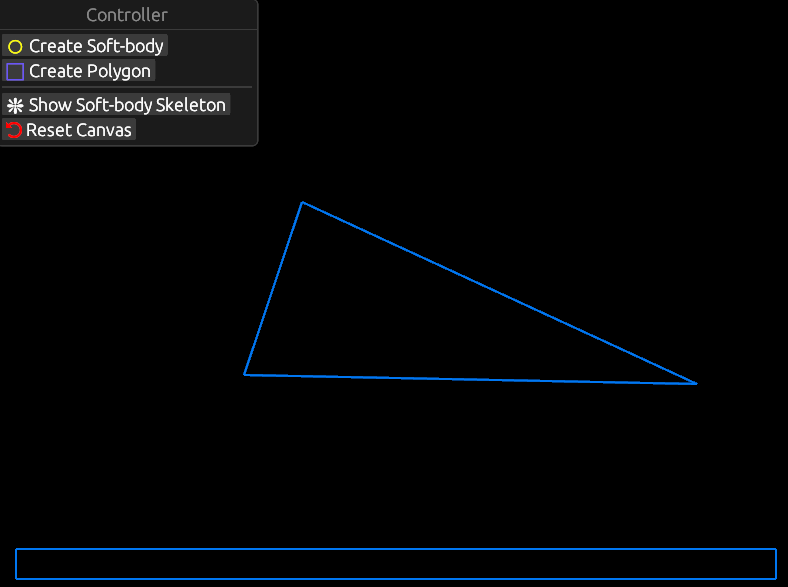
You can generate new soft-bodies

And change the geomtery of the environment

Try it youself!

You can visit the hosted version or cargo run to run locally (cargo required ofc).

Physics stuff

The soft body model

I went with a very basic spring-mass model, with a traditional spring connection pattern with triangles to mantain the shape of the structure.

The springs follow Hooks low with damping, so we can get the total force exerted by a single spring with:

• the stiffness factor of the spring ($k_s$)
• the damping factor of the spring ($k_d$)
• the resting length of the spring ($L_0$)
• the positions ($A$, $B$) and velocities ($v_A$, $v_B$) of the masses at the edges of the spring $$F_{tot} = k_s \cdot(|B-A| - L_0) + k_d \cdot\left(\frac{B-A}{|B-A|}\right)\cdot(v_b - v_a)$$

Motion integration

Of the many existing iterative methods to calculate the approximate solution of the motion integration, I went with the classic Runge-Kutta method, because of its high accuracy, which is critical for the fight against self collision and tunnelling.

Given the general definition of the Runge-Kutta method of order $n$, with a time step size $h$

$$y_{t+h} = y_t + h\cdot\sum_{i=1}^{n}{a_ik_i} + O(h^{n+1})$$

we can evaluate the fourth order and find the coefficients of the sum as: $$a_1 = \frac{1}{6}, \ \ a_2 = \frac{1}{3}, \ \ a_3 = \frac{1}{3}, \ \ a_4 = \frac{1}{6}$$

Every slope of the integration ($k$) can be calculated through the midpoint of the previous one.

$$ \begin{aligned} & k_1 = hf(t, y_t) \\ & k_2 = hf(t + \frac{h}{2}, y_t + \frac{k_1}{2}) \\ & k_3 = hf(t + \frac{h}{2}, y_t + \frac{k_2}{2}) \\ & k_4 = hf(t + h, y_t + k_3) \end{aligned} $$

So the final formula will be: $$y_{t+h} = y_t + \frac{1}{6}k_1 + \frac{1}{3}k_2 + \frac{1}{3}k_3 + \frac{1}{6}k_4$$

Or, even better: $$y_{t+h} = y_t + \frac{1}{6}(k_1 + 2k_2+ 2k_3 + k_4)$$

We'll iteratevely run this calculation with the motion obtained by the spring force represented as the function $f$

TODOs

• Prevent self collision
• Add friction between masses and polygons
• Add bend and shear mechanics